 In the NISQ era, it is difficult to perform quantum algorithms due to the many sources of errors that impact performance and reduce accuracy. Imprecise control pulses and classical EM crosstalk result in imperfect unitary operators, leading to coherent errors, whereas interactions with a noisy environment result in incoherent errors. Coherent errors can be particularly detrimental to algorithm performance due to the fact that they can accumulate quadratically with circuit depth. On the other hand, stochastic errors, such as bit or phase flips, only accumulate linearly with circuit depth. One method of improving algorithm performance on noisy quantum processors is through Randomize Compiling (RC) [1], a QCVV protocol which tailors coherent errors into stochastic Pauli errors during the implementation of a quantum circuit or algorithm. By compiling single-qubit twirling gates randomly sampled from some set into the bare sequence of an algorithm in such a way that the overall logic remains unchanged, and then combining the results of many different logically-identical circuits, the effect of coherent errors on the gates in the original circuit are averaged into stochastic noise channels that are independent of the gates themselves. Previous theoretical work [1] demonstrated RC improvement in simulation results for multi-qubit circuits.
In the NISQ era, it is difficult to perform quantum algorithms due to the many sources of errors that impact performance and reduce accuracy. Imprecise control pulses and classical EM crosstalk result in imperfect unitary operators, leading to coherent errors, whereas interactions with a noisy environment result in incoherent errors. Coherent errors can be particularly detrimental to algorithm performance due to the fact that they can accumulate quadratically with circuit depth. On the other hand, stochastic errors, such as bit or phase flips, only accumulate linearly with circuit depth. One method of improving algorithm performance on noisy quantum processors is through Randomize Compiling (RC) [1], a QCVV protocol which tailors coherent errors into stochastic Pauli errors during the implementation of a quantum circuit or algorithm. By compiling single-qubit twirling gates randomly sampled from some set into the bare sequence of an algorithm in such a way that the overall logic remains unchanged, and then combining the results of many different logically-identical circuits, the effect of coherent errors on the gates in the original circuit are averaged into stochastic noise channels that are independent of the gates themselves. Previous theoretical work [1] demonstrated RC improvement in simulation results for multi-qubit circuits.
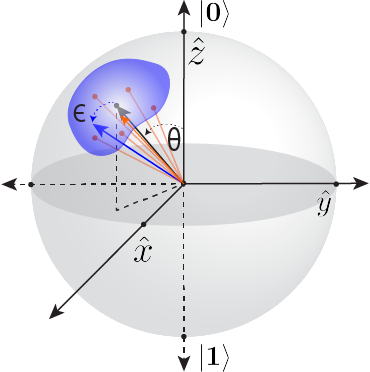
The intuition behind how RC improves algorithm accuracy can be understood with the following argument, illustrated in the figure under “What we did”: Consider the final state of a single-qubit after performing a sequence of gates. The ideal final state (black vector) will lie somewhere on the surface of the Bloch sphere. The ensemble measurements of this final state will yield a probability distribution of 0’s and 1’s, which depends on where the final state of the Bloch vector is before measurement. In a circuit dominated by coherent errors, the actual final state of a bare circuit (blue vector) will be separated from the ideal state by some distance (blue surface area) due to the accumulation of over- or under-rotations during the sequence of gates. When we perform RC on a circuit, we randomize the effect that coherent errors have on the same logical circuit, so any given instance of a single RC circuit (orange points) will also be distinct from the ideal state. However, the combined distribution of all of the different RC circuits results in an average state (orange vector) that is much closer to the ideal state than is the bare state. In essence, each RC circuit represents a distinct trajectory to the same final state, and averaging together all of these trajectories mitigates the effect of coherent errors on the algorithm.
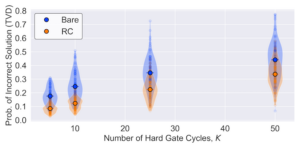
To evaluate the efficacy of RC, we calculate the Total Variational Distance (TVD) of the measured bare and RC ensemble probability distributions with respect to the ideal distribution. The TVD simply computes the difference between two probability distributions, where 0 indicates that they are identical, and 1 indicates that there is no overlap. Since a lower TVD is better when it comes to performing algorithms, it can also be interpreted as the probability of measuring the incorrect solution of a circuit. Therefore, if RC is successful, it will have a lower TVD than the bare circuit. The ideal distribution can be computed classically for most algorithms and circuits involving smaller numbers of qubits and shorter circuit depths, but this becomes intractable as the size and complexity of quantum circuits increases.
• Tomography of Randomized Compiling
To verify this intuitive picture of RC, we performed state-tomography on a single random bare circuit and on the RC circuits. The bare circuit was divided into three different circuit depths: near the beginning of the circuit, halfway through the circuit, and at the end of the circuit. For each of these bare circuit depths, we generated 20 different RC circuits. The idea was to visualize the progressive improvement of RC as more coherent error accumulated in the bare circuit. These single-qubit tomography results can be seen in one of the project posts.
• Random Circuit Sampling
To demonstrate how RC scales as a function of number of qubits, circuit depth, and amount of coherent error, we sampled many different random circuits and compared their bare and RC TVDs. For each experiment, we generate random circuits of several different circuit depths to see how RC improvement changes as more coherent errors build up. Here, we define circuit depth as K cycles of interleaved “easy” and “hard” gates. For single-qubit circuits, easy gates are defined to be the Clifford set, and hard gates are any non-Clifford gate. For the graph shown above the Project Description, we performed single-qubit gates simultaneously on four qubits. For each circuit depth, we generated 100 different random circuits, and for each random circuit we generated 20 RC circuits. Violin plots are used to give a sense of the shape of the bare and RC distributions at each circuit depth. The results conclusively show that RC reduces the average probability of measuring the incorrect solution for all circuit depths.
Current Status & Next Steps
In this experimental work, we have demonstrated that, in the majority (> 85%) of circuits containing some amount of coherent error, the final measured result is more accurate when using Randomized Compiling. This is true for any number of qubits and all circuit depths tested. Furthermore, we have demonstrated that we only needed a fraction of the total number of randomly compiled circuits in order to converge to an optimal result: only ~5 – 10 RC circuits were needed, compared to the 20 that were actually used (see the relevant project post under the Latest News). This is promising for those wanting better accuracy without the added expense of longer runtimes. Finally, by performing tomography on bare and RC circuits, we have provided an intuitive picture of how RC works, namely that the final state of any real implementation of a circuit can be represented by a vector on the Bloch sphere, and this vector in a noisy circuit is located further from the ideal final state than the state represented by the union of all of the individual RC results.
• Extend the maximum possible circuit depth via noise tailoring
• Use Cycle Benchmarking to benchmark and mitigate errors in multi-qubit cycles, and estimate the tailored error rate when a circuit is performed under RC
• Demonstrate the advantages of RC on known quantum algorithms