 Variational Quantum Eigensolver (VQE) algorithms have attracted a lot of interest recently because of the good results obtained on the NISQ hardwares (some relevant experimental implementations are listed below). They however require the use of an ansatz, which constrains the part of the Hilbert space which can be spanned with the VQE. The choice of the ansatz remains a complicated problem, and the classical part of the algorithm also requires an optimization.
Variational Quantum Eigensolver (VQE) algorithms have attracted a lot of interest recently because of the good results obtained on the NISQ hardwares (some relevant experimental implementations are listed below). They however require the use of an ansatz, which constrains the part of the Hilbert space which can be spanned with the VQE. The choice of the ansatz remains a complicated problem, and the classical part of the algorithm also requires an optimization.
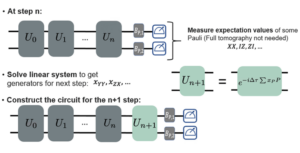
The QITE algorithm works differently because such an ansatz is not needed. At each timestep (which is computed from the results of the previous one), the imaginary time evolution brings the prepared state closer to the ground state. There is no ansatz, but the drawback is that the circuit size increases. As soon as the state we start with has some overlap with the ground state, the state should converge to it.
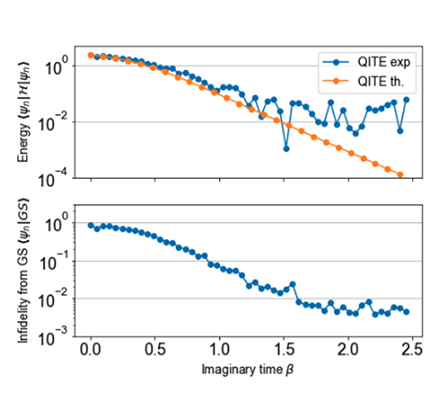
We implemented the QITE algorithm on the 2 qubit Ising model, as is done in Motta et al., Nature Physics (2020). We found a similar behaviour as they obtained implementing it on the Rigetti machine available online: some jumps in energy occurring because of the noise. Several trajectories had to be averaged to extract a result.
Using noise mitigation techniques, we managed to improve the stability of the algorithm, reaching the ground state in energy and fidelity with a precision below 1%.
Current Status & Next Steps
Motivated by the improvement seen for 2 qubits, we are planning to scale up the implementation of the algorithm, going to 3 and 4 qubits. We also plan to do thermal simulations with the QMETTS algorithm, also described in the Motta et al. (2020) paper.