 As the number of qubits and the depth of quantum circuits increases, quantum systems become more vulnerable to errors. These errors can be mitigated by the use of quantum error correction protocols. Many correction protocols require the measurement of certain operators known as stabilizers, which quantize and detect errors, followed by the application of a gate correcting the error.
As the number of qubits and the depth of quantum circuits increases, quantum systems become more vulnerable to errors. These errors can be mitigated by the use of quantum error correction protocols. Many correction protocols require the measurement of certain operators known as stabilizers, which quantize and detect errors, followed by the application of a gate correcting the error.
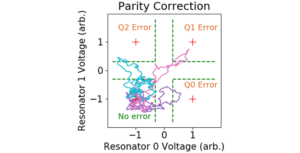
One method to implement such a scheme is to couple multiple transmons to joint readout resonators and map stabilizers of the transmons directly onto the frequency of these resonators. This frequency may then be probed by an always-on microwave drive, giving continuous information about the state of the stabilizers. The current experiment includes three qubits and two resonators connecting the qubits pairwise. By probing the resonators, we monitor the parity of the first two qubits, , and the parity of the second two qubits, , allowing us to stabilize subspaces of constant parity (such as {|000>, |111>}) against single bit flips. For example, if we prepare the state |000> and sometime later see that the response of the first resonator changes, but the response of second resonator stays the same, we infer that the state has changed to |100>. Using classical room temperature electronics, we can detect any such bitflips which occur and apply real time correction pulses to the system, restoring the original state.
What We Did
TBD
Current Status & Next Steps
TBD